Comment calculer le rayon d’un cercle à partir d’une corde ?

Géométrie : Cercles Définition

Un cercle est une figure plate regroupant l’ensemble des points équidistants à un point donné. Ce point est appelé le centre du cercle. Le cercle peut être dessiné via une boussole. Ce dernier permettra en fixant le centre, de dessiner l’ensemble des points situés équidistants de ce centre. La seule différence entre les cercles est définie par rapport au rayon et donc par rapport à la taille du cercle. Les éléments suivants sont définis pour un cercle :

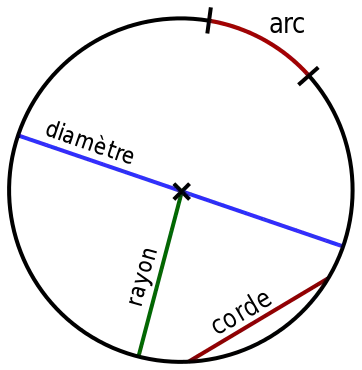
• Rayon correspond à un segment reliant le centre et un point du cercle
• Le diamètre correspond à un segment reliant deux points du cercle, passant nécessairement par le centre. Sa distance correspond à deux fois celle du rayon
• Une corde est un segment reliant deux points du cercle
• Un arc d’un cercle correspond à une partie du contour du cercle
• Le périmètre d’un cercle correspond à la longueur du contour du cercle. Ce dernier est calculé à l’aide de la formule suivante : Périmètre = 2*π*R avec R étant le rayon du cercle
• La zone d’un cercle correspond au volume à l’intérieur du cercle. Il est calculé à l’aide de la formule suivante : Aire = π*R*R, R étant le rayon du cercle

Lire également : Comment choisir la puissance d'une pompe de piscine

Représentation des différentes propriétés du cercle Tangent à un cercle

Soit à un point du cercle C du centre O. La tangente au cercle en A est la ligne ne passant que par le point A du cercle. Cette tangente au cercle conduit à certaines propriétés :

• Grâce au point A du cercle C au centre O, nous pouvons construire le segment. La tangente au cercle sera nécessairement la ligne correspondant à la perpendiculaire du segment. Il peut ainsi être tracé en tracant la ligne perpendiculaire au rayon passant par A.
• Par la réciproque, si une ligne est perpendiculaire au segment, elle correspond nécessairement à la tangente au cercle en A

Où puis-je trouver des cours de mathématiques à examiner avant un événement ?

A voir aussi : Conversion rapide : 1/4 litre en ml - Comprendre les mesures de volume

Angles et coins Runique au centre

Théorème du coin au centre :

Soit H est un point du cercle C du centre O. Être A et B deux points distincts sur le cercle. Si les angles AHB et AOB interceptent le même arc de cercle correspondant à AB, alors nous avons : $2  widehat {AHB} =  widehat {AOB} $

Théorème d’angle Runique

Laissez M un point de cercle C du centre O et rayon R. Soyez A et B deux points distincts sur le cercle. L’angle $  widehat {AMB} $ est inscrit dans le cercle.

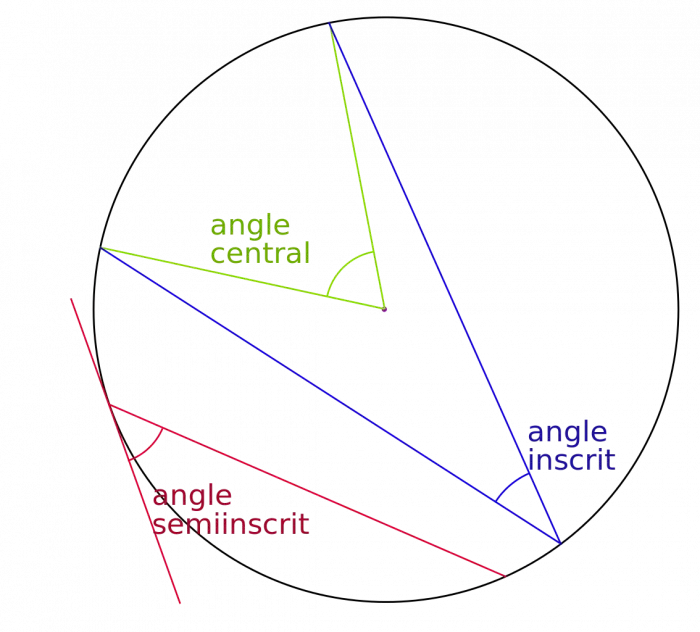
Représentation de l’angle inscrit et de l’angle au centre Triangle rectangulaire et cercle

Au cours des mathématiques en ligne, on dit qu’un triangle est circonscrit à un cercle lorsqu’il est compris dans le cercle. Les trois points du triangle correspondent alors à 3 points du cercle C.

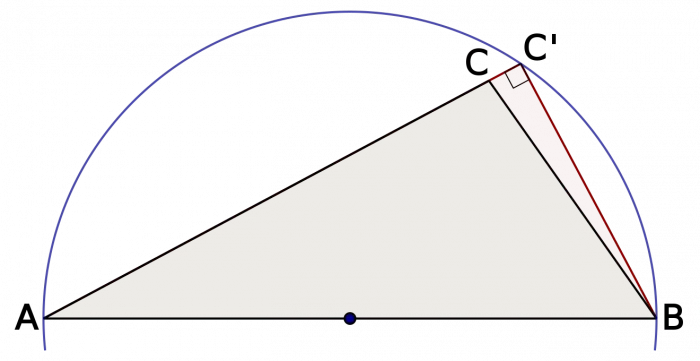
Si un triangle rectangle est circonscrit à un cercle, alors son hypoténuse est un diamètre du cercle circonscrit. En passant :

• Le milieu de l’hypoténuse du triangle rectangle correspond au point O, à savoir le centre du cercle C

• La longueur du segment correspondant au sommet de l’angle droit a la même longueur que la moitié de l’hypoténuse et donc la même longueur que le rayon du cercle.

Par réciproque, si un triangle est circonscrit au cercle du centre O, et que l’hypoténuse de ce triangle correspond au diamètre du cercle circonscrit, alors ce triangle est rectangle.

Le bon AB passe par le centre du cercle. AB est un diamètre du cercle. Exercices corrigés

EXERCICES

Exercice 1 Soit un quadrilatère ABCD formé de telle sorte que les lignes (BD) et (CD) soient tangentes au cercle central A. Quelle est la nature de la quadrilatère ABCD.

Exercice 2

• Laissez C un cercle de centre A et rayon R = 5cm.
• Soit EF un diamètre du cercle C.
• Laissez M un point du segment tel que AM = 4cm.
• Laissez P un point du cercle tel que MP = 3cm

Démontrer que le triangle AMP est un triangle rectangulaire en M

Exercice 3

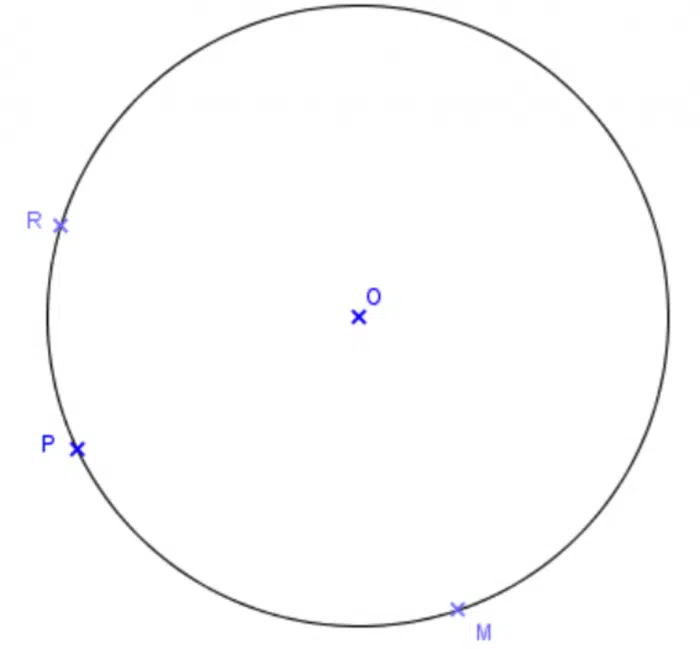
Soit le cercle C du centre O et les points R, P et M des points du cercle C. Ces points sont indiqués dans la figure suivante :

Les points R, P, M du cercle 1. Nous savons que l’angle $  widehat {ROP} $ mesure 60 degrés. Déterminer la mesure d’angle $  widehat {RMP} $

2. a) Déterminer la représentation de l’arc intercepté par l’angle inscrit $  widehat {RPM} $

b) Déterminer quel angle est associé au centre $  widehat {ROM} $

c) Sachant que l’angle $  widehat {RPM} $ mesure 100 degrés, déterminez le mesure de l’angle central associé à l’angle $  widehat {RPM} $

Corrigé

Exercice 1

Au centre du cercle C. La ligne droite (BD) est tangente au cercle du centre A, puis nous avons une perpendiculaire entre la longueur venant de A et la ligne droite (BD). En ce qui concerne la ligne droite (CD), cette dernière étant aussi la tangente au cercle central A, nous avons aussi une seconde perpendiculaire.

Nous avons donc deux lignes perpendiculaires et deux distances correspondant au rayon et étant donc de la même longueur. Ceci correspond à la définition du carré.

Le quadrilatère ABCD est donc carré .

Exercice 2

1. Pour démontrer qu’un triangle est rectangle, nous pouvons utiliser le théorème de Pythagore. Selon ce dernier, un triangle ABC est rectangle lorsque la somme $AB^ {2} AC^ {2} = BC^ {2} $ avec BC étant l’hypoténuse de le triangle.

P étant un point du cercle, la longueur AP est égale au rayon du cercle, c’est-à-dire AP = 5cm. Nous voulons maintenant vérifier par le théorème de Pythagore si le triangle est rectangle.

$AM^ {2} MP^ {2} = 3^ {2} 4^ {2} = 9 16 = 25$

$AP^ {2} = 5^ {2} = 25$

Nous avons $AP^ {2} = AM^ {2} MP^ {2} $. Selon la réciproque du théorème de Pythagore, le triangle AMP est rectangulaire en M.

Exercice 3

1. La mesure d’angle $  widehat {ROP} $ correspond à la mesure d’angle au centre et est associée à l’angle inscrit $  widehat {RMP} $. La mesure d’angle $  widehat {RMP} $ est donc égale à la mesure de l’angle $  widehat {ROP} $ ou 60 degrés.

2.a. La représentation de l’arc de l’angle $  widehat {RPM} $ correspond simplement à l’arc du point R au point M (passant par le point P).

2.b. Pour déterminer l’angle central associé au $  widehat {RPM} $ angle, vous devez d’abord tracer les deux segments RO et OM. Une fois ces segments tracés, l’angle au centre de RPM représente le grand angle de la ROM.

2.c. Sur la base de la formule d’angle central, la mesure de RPM est égale à la moitié de la mesure d’angle au centre ROM. Donc, nous obtenons

$  widehat {RPM} =  frac {  widehat {ROM}} {2}  Leftrightarrow  widehat {ROM} = 2*  widehat {RPM} $ = 2*100 = 200 degrés.

La mesure de l’angle ROM est donc égale à 200 degrés.